|
("Мистика" коротких антенн продолжается…)
В.Т.Поляков
Февраль-март 2003 г.
Постановка задачи. Когда автор, вовсе не преследуя далеко идущих целей, а просто ради курьеза и для души занялся детекторными приемниками, которые скоро стали громкоговорящими, он и предположить не мог, какие новые “открытия” ждали его на этом пути. Кавычки здесь поставлены потому, что очень хорошо разбирающийся в теории и практике антенн специалист с полным правом может сказать, что ничего нового не открыто, тем не менее то, о чем пойдет речь, трудно назвать общеизвестным.
Попытка посчитать мощность, которую можно извлечь из эфира с помощью короткой (по сравнению с длиной волны) антенны, привела к выводу формулы
P0 = E2l2/6400,
где E — напряженность поля у антенны, l — длина волны, на которую антенна настроена. Формула пригодна для антенны без потерь, размещенной над идеально проводящей землей и отдающую всю принятую мощность в нагрузку (приемник) [1].
Из формулы следует, что в радиусе 100 км от 500-киловаттной ДВ радиостанции теоретически можно извлекать из эфира ватты (!) мощности, а уж милливатты, нужные для громкоговорящего приема — в радиусе тысячи километров!
Публикация прошла после немалой полемики, и решающим был довод автора: если малая передающая антенна без потерь излучает всю подводимую мощность (а куда же ей еще деться?), то по теореме взаимности и приемная антенна должна развивать на нагрузке указываемую формулой мощность, причем независимо от размеров антенны. Этот довод и был дан в комментарии от редакции.
Однако реальные, построенные в любительских условиях приемные ДВ антенны имеют КПД не выше долей, или в лучшем случае единиц процентов, и отдают мощность, на два-три порядка меньше теоретической, что иногда, впрочем, тоже немало.
Что надо сделать, чтобы улучшить ситуацию? Вопрос важен для всех, занимающихся радиоприемом и связью на ДВ. Рекомендации известны: увеличивать размеры антенны и снижать потери в проводах, окружающих предметах и заземлении. В результате придем к конструкции приемной антенны, вполне сравнимой с передающей (стометровые мачты, толстые провода и закопанные в землю сотни килограммов меди для хорошего заземления). Нет сомнения, что теоретически предсказанная мощность будет извлечена из эфира, но какой ценой!
Для поиска приемлемых решений придется досконально разбираться в физике работы антенн. Итак, идеальная малая антенна без потерь может извлекать из эфира значительную мощность, но как она это делает? Вопрос открыт.
Парадокс. Известно, что приходящее к антенне электромагнитное поле несет энергию, причем плотность ее потока (вектор Умова—Пойнтинга)
П = E.H = E2/120p = E2/377,
где 120p = 377 Ом — волновое сопротивление свободного пространства. Чтобы извлечь из приходящего поля мощность Р, антенна должна обладать некоторой эффективной поверхностью Sэфф, тогда
P = П.Sэфф = Е2Sэфф/377.
Поверхность Sэфф легко найти, приравняв два приведенных выражения для мощности: E2 l2/6400 = Е2Sэфф/377. Отсюда получаем:
Sэфф » 0,06 l2 » 0,5(l/3)2.
Выходит, что маленькая антенна без потерь обладает внушительной эффективной поверхностью, намного превосходящей ее реальную поверхность, примерно l/4 ´l/4. На ДВ она может составить примерно полкилометра на полкилометра! В то же время для проволочных антенн о “площади” тонкого провода говорить вообще не приходится. Этот парадокс просто необходимо как-то объяснить. Посмотрим сначала, что сделано в других областях радиофизики и смежных наук применительно к нашему вопросу.
Экскурсия в радиофизику. В случае СВЧ антенн, для которых справедливы приближения геометрической оптики, дело обстоит просто. Представим себе рупор, направленный в сторону передатчика (рис. 1). Мощность Р, попадающая в раскрыв рупора площадью S, и равная П.S, собирается в волноводную (или другого типа) фидерную линию и направляется в нагрузку (приемник) R. Если рупор хорошо спроектирован (т. е. искажения поля в раскрыве пренебрежимо малы), а линия хорошо согласована, то в этой системе отражений не будет, и вся мощность Р поглотится приемником. Sэфф такого рупора равна геометрической площади его раскрыва S.

Интересно, если передатчиком послужит радиолокационная станция, увидит ли она наш согласованный рупор, направленный на нее? Ответ очевиден — радар улавливает лишь отраженные сигналы, а отражений-то в нашей системе и нет. На экране радара рупор будет выглядеть черным пятном, поскольку поглощает все падающее на него излучение.
В ИК технике широко пользуются понятием абсолютно черного тела (АЧТ), не отражающего падающую на него энергию. Выполняют его в виде полой сферы, покрытой изнутри поглощающим материалом (хороша даже печная сажа). Излучение, многократно переотражаясь стенками сферы, и каждый раз ослабевая, поглощается практически полностью (рис. 2).
В астрономии есть гипотеза о существовании во вселенной “черных дыр”, не отражающих и не излучающих из-за очень сильного гравитационного поля (поэтому и увидеть их нельзя). Вычисляют даже радиус некоторого объема (сферы Шварцшильда), при попадании в который ни вещество, ни излучение обратно выйти уже не могут.
Бог с ним, с веществом, нам бы разобраться с излучением. Может ли приемная антенна излучать? Если стенки АЧТ (рис. 2) сделать не черными, а зеркальными, то энергия поглощаться не будет, и после нескольких переотражений внутри сферы ИК излучение выйдет обратно. Чтобы создать мощное отражение в том направлении, откуда приходит излучение, помещают три плоских зеркала под углом строго 90о друг к другу (рис. 3). Уголковые отражатели широко применяются и на СВЧ, в радиолокации, и на более коротких ИК волнах, и на еще более коротких волнах в оптике.
Вернемся к рис. 1. Малейшее отражение в фидере или нагрузке приведет к тому, что часть мощности отразится и будет переизлучена приемной антенной обратно в эфир. Теперь радар увидит приемную антенну. А если перегородить волновод отражающей заслонкой О (замкнуть или оборвать кабель)? Коэффициент отражения станет равным единице, и вся принятая мощность излучится обратно, с учетом коэффициента направленного действия рупора. “Черная дыра” на экране радара превратится в яркую точку.
По этому принципу тоже выполняют некоторые радиолокационные отражатели-маяки, но в отличие от уголковых, они отражают туда, куда направлен рупор. Более того, если модулировать отраженное излучение, например, полупроводниковым диодом, можно организовать линию радиосвязи без передатчика на передающей стороне. Вывод из сказанного ясен — приемная антенна должна быть согласованной.
Однако, в рассмотренных случаях размеры антенн велики по сравнению с длиной волны. Заметим также, что все перечисленные устройства широкополосны. Нет ли в физике случаев, когда эффективно работают именно малые антенны? Оказывается есть, и сколько угодно. Начнем с самых коротких электромагнитных волн — гамма лучей.
Известен эффект Мессбауэра, или ядерный гамма-резонанс, при котором ядра атомов излучают или поглощают кванты лишь строго определенных энергий, а следовательно и частот (энергия e связана с частотой f формулой Планка: e = hf, h — константа). Заметим, что длина волны гамма излучения намного больше размеров ядра.
При описании ядерных реакций, вызванных бомбардировкой ядер частицами, вводят понятие эффективного поперечного сечения реакции s (с размерностью в барнах, 1 барн = 10 -28 м2), характеризующее эффективность захвата частиц ядрами. Графики зависимости s от энергии частиц e нередко удивительно напоминают резонансные кривые колебательного контура, посмотрите картинки в любом учебнике, а взаимодействие так и называют — резонансным. Сравните sи Sэфф. Фактически, это одно и то же!
Двинемся в сторону длинных волн — в оптическом и ИК диапазонах сплошь и рядом резонансное поглощение, резонансное излучение. Лазер дает монохроматическое (одночастотное, с узким спектром) излучение только потому, что использует резонансные переходы атомов с одного энергетического уровня на другой: hf = e1 – e2. Но размеры атомов примерно на четыре порядка меньше длины волны. Ситуация показана на рис. 4, но чтобы масштаб был правильным, размеры кружочка-атома надо уменьшить еще в тысячи раз.
На сантиметровых и миллиметровых волнах связи и локации очень мешает поглощение в атмосфере, поэтому выбирают “окна прозрачности” вдали от резонансных спектральных линий поглощения водяного пара (1,35 см или 22 ГГц), кислорода (около 6 мм или 50 ГГц) и т. д. Но размеры молекул составляют несколько ангстрем (1 А = 10 -10 м), здесь они уже на 7 порядков меньше длины волны! Тем не менее эти маленькие молекулы — “антенны” эффективно взаимодействуют с проходящей волной, поглощая ее, т. е. делают то же самое, чего и мы хотим от нашей приемной ДВ антенны. Излучение и поглощение сугубо резонансное, причем спектральные линии очень узкие, что говорит о высокой добротности атомных резонансных систем, не зря же их используют в эталонах частоты. Лишь при поглощении в атмосфере линии поглощения уширяются из-за теплового движения молекул.
Итак, второй вывод: малая антенна должна быть резонансной.
Вернемся к нашим антеннам. Эка, вывел! — скажет читатель. А мы что делаем? Даже в детекторном приемнике мы настраиваем антенну в резонанс с помощью колебательного контура (с которым она сильно связана) и затем подбираем связь с детектором, согласуя его входное сопротивление с пересчитанным в контур сопротивлением антенны. Что же, пока наши выводы только подтвердили то, к чему давно уже пришли практически.
Но каков должен быть резонанс антенны? Тупой при сильной ее нагрузке, или наоборот, острый? Мера резонансных свойств антенны — ее добротность, которую проще всего определить по полосе пропускания антенны вместе с ее согласующей цепью (контуром):
Q= f0/2Df,
где f0 — резонансная частота, Df — расстройка, при которой напряжение сигнала, снимаемого с антенны, падает до 0,7, а мощность до 0,5 от значений, полученных при резонансе.
В [2] была показана высокая эффективность коротких антенн при приеме, в случае, когда собственные потери антенной цепи малы или скомпенсированы положительной обратной связью (регенерацией). Добротность при этом получается высокой, напряжение на антенне большим, а собственное поле антенны оказывается значительно сильнее внешнего. В ряде практических экспериментов даже без регенерации были получены напряжения на антенне до 100 В при напряженности падающего поля 0,1...0,2 В/м.
Затем было установлено, что малые электрические и магнитные антенны одинаково эффективны при одинаковых объемах их ближних полей, хотя и согласовываются с генератором или нагрузкой совершенно по-разному [3].
Наконец, было выяснено, при каких условиях малая антенна может быть эффективной. Оказалось, что добротность антенного контура Q должна возрастать обратно пропорционально объему, занимаемому ближним полем антенны, или кубу ее линейных размеров.
Была выведена формула, связывающая объем ближнего поля V и добротность Q эффективной (т. е. имеющей КПД, близкий к 100%) малой антенны в свободном пространстве [4]:
Q0 = l3/26V.
Добротность была взята как отношение реактивного сопротивления антенны к удвоенному сопротивлению излучения, удвоенному потому, что либо антенна нагружена на входное сопротивление приемника, равное сопротивлению излучения по условиям согласования, либо питается от передатчика с таким же выходным сопротивлением.
Перепишем последнюю формулу несколько по-другому, чуть-чуть округлив коэффициент (ведь наши формулы носят приближенный, оценочный характер):
VQ = (l/3)3.
Еще учтем, что объем поля рассматриваемой здесь заземленной антенны вдвое меньше (поле сосредоточено только в верхнем полупространстве):
VQ = 0,5(l/3)3.
По обе стороны знака равенства теперь стоят объемы — слева объем поля идеальной заземленной антенны, увеличенный в Q раз из-за ее резонансных свойств. Ему уместно дать название резонансный объем поля антенны
VQ = Vp.
Справа стоит объем, связанный с длиной волны. Назовем его
V0 = 0,5(l/3)3.
Это тот объем, из которого антенна должна черпать энергию, чтобы удовлетворять самой первой формуле нашей статьи, выведенной в [1].
Но почему мы теперь говорим об объемах, а не об эффективной поглощающей поверхности? Автора привели к этому сами математические выводы, и когда они были сделаны, оказалось, что и с физической точки зрения гораздо лучше говорить об объемах, ведь малая антенна отбирает энергию волн со всех сторон, а ее ближнее поле имеет конфигурацию, близкую к несколько вытянутой вверх полусфере (кстати, эта форма не имеет ничего общего с диаграммой направленности).
Легко можно показать, что объемная плотность энергии приходящего к антенне электромагнитного поля (e0E2) и плотность потока его энергии (E2/120p) пропорциональны друг другу (связаны через постоянный коэффициент, равный скорости света c = 1/Öm0e0), а принимаемая антенной мощность как раз и пропорциональна Е2.
Теперь у нас обрисовалась следующая физическая картина (рис. 5): если антенна не мала, и объем ее ближнего поля V равен V0, то она может иметь единичную добротность и быть широкополосной. Например, антенна может представлять собой вертикальный провод с емкостной нагрузкой, как на рис. 5, или конус, направленный вершиной к земле. Но тогда и размеры антенны велики. Если же мы значительно уменьшили размеры антенны, и V также уменьшился, то мы должны увеличить добротность настолько, чтобы резонансный объем поля достигал V0. Вот и получается, что добротность идеальной антенны обратно пропорциональна объему.

Посмотрим теперь, что будет, если антенна не идеальна, т. е. если она имеет, кроме сопротивления излучения, еще и некоторое сопротивление потерь, не связанное с отдачей мощности в приемник. Добротность антенны, естественно, уменьшится, и, соответственно, сократится ее резонансный объем VQ. Добротность и КПД уменьшаются пропорционально друг другу, поэтому КПД оказывается равным:
h = Vp/V0.
Эта замечательная и предельно простая формула (кстати, никогда ранее не встречавшаяся автору) имеет очень простой и ясный физический смысл: если резонансный объем поля антенны не достигает необходимого для отбора теоретически возможной мощности (V0), то КПД антенны уменьшается, и принятая мощность становится равной:
Р = Р0.h.
Ближнее поле. Поговорим теперь подробнее о свойствах ближнего поля антенны. Во-первых, оно квазистатическое, т. е. его можно рассчитывать (для рассматриваемой электрической антенны) методами электростатики. Например, если вертикальная антенна имеет верхнюю емкостную нагрузку (диск, зонтик, система горизонтальных проводов), то ее ближнее поле подобно полю заряженного конденсатора, образованного нагрузкой и землей. Во-вторых, это поле реактивное, т. е. не расходует энергию ни на излучение, ни на потери, а как бы запасает ее. Действительно, по другому определению добротность — это отношение запасенной энергии к энергии, расходуемой за период колебаний (на излучение при передаче и в нагрузке при приеме).
Разумеется, ближнее поле не имеет резких границ, показанных на рис. 5, оно спадает плавно при удалении от антенны. Установив закон изменения поля в разных направлениях от антенны, можно найти его эффективный объем (придется вычислять тройные интегралы в сферических координатах, но для математиков это не составляет особой трудности). В курсах электростатики доказано, что поле диполя (а у нас половинка диполя) спадает по закону 1/r3 (рис. 6). Это весьма примечательно, и позволяет сделать еще один важный вывод.
Возьмем полноразмерную ненагруженную антенну с объемом ближнего поля V0 и Q = 1 (рис. 7,а). Приходящая волна наведет в антенне ЭДС, равную E.hд, и таким же будет напряжение сигнала на верхней емкостной «шляпе» антенны. Собственное поле антенны найдем, разделив напряжение на высоту hд. Его напряженность составит Е, т. е. будет равна напряженности внешнего поля.
Уменьшив размеры антенны, к примеру, в 10 раз, мы уменьшим объем ближнего поля в 1000 раз (рис. 7,б). Теперь придется включить «удлиняющую» катушку L с добротностью значительно более 1000 (см. выше) и настроить антенну в резонанс, учитывая меньшую емкость «шляпы». ЭДС, наведенная полем принимаемой волны стала меньше в 10 раз, и во столько же раз уменьшилось расстояние между обкладками конденсатора hд. Но из-за большой добротности напряжение на «шляпе» возрастет в 100 раз, а собственное поле антенны под «шляпой» — в Q, т. е. в 1000 раз!
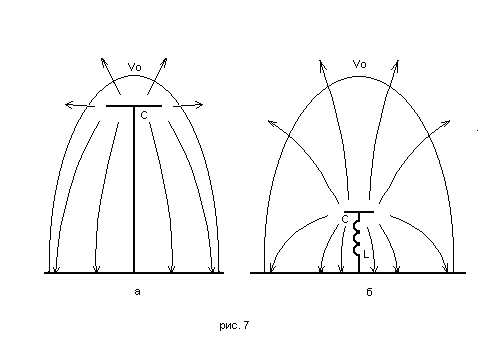
При удалении от антенны на 10 ее размеров собственное поле, убывая по закону 1/r3, станет равным Е, как и в прежнем случае полноразмерной антенны. Таким образом, мы выяснили физический смысл объема V 0 — на его границе собственное поле антенны без потерь равно внешнему. В центре этого объема, у самой антенны, собственное поле антенны будет в Qраз сильнее внешнего.
Ненагруженная антенна будет переизлучать принятый сигнал по всем направлениям, в соответствии со своей хорошо известной диаграммой направленности — максимум на горизонт и нуль вверх. Если мы захотим еще увеличить добротность антенны, у нас это вряд ли получится — помешает сопротивление излучения. Другими словами, антенна просто сбросит «лишнюю» мощность в окружающее пространство. То же произойдет, если подключить к антенне регенератор — неплохая идея регенеративного ретранслятора, не так ли?
Нагрузим антенну сопротивлением, равным сопротивлению излучения. Напряжение на антенне составит половину наведенной ЭДС и собственное поле антенны уменьшится вдвое. Соответственно, уменьшится и переизлучение энергии антенной, половина мощности направится в нагрузку.
Последний вывод, который уже напрашивается из изложенной теории, таков: малая антенна черпает энергию из приходящего электромагнитного поля посредством своего ближнего реактивного собственного поля, которое создается путем накопления принятой энергии в высокодобротной колебательной системе самой антенны.
Добавление первое — историко-библиографическое.
Материал был готов в ноябре 2002 г, но прочитавшие его сделали ряд замечаний, часть которых сводилась к тому, что говорить об объемах, занимаемых полями антенны незачем, взаимодействия полей нет, а если бы было, то кто-нибудь об этом бы уже написал. Оказывается, писали, и неоднократно.
Гипотезу о взаимодействии приходящего поля с собственным полем антенны (благодаря чему и извлекается энергия) выдвинул Р. Рюденберг, один из основателей теории антенн, еще в 1908 году [5]. Кстати, его именем долго называли формулу для сопротивления излучения короткой антенны.
Детальный анализ взаимосвязи добротности и объема антенны выполнил Чу в 1947 году [6], установив обратную пропорциональность добротности и куба линейных размеров. Использованный математический аппарат (интегрирование по сферическим гармоникам) весьма сложен. Выведенный им объем V0 (для антенны в свободном пространстве) составил (l/p)3, что хорошо согласуется с результатом [4], полученным с помощью элементарной алгебры, (l/3)3.
В статье Хансена [7] показано, что если малая, но эффективная антенна вместе с передатчиком заключена внутри сферы радиусом r, то ее добротность не может быть меньше примерно (l/2pr)3. Таким образом, выводы, приведенные в данной статье, давно получены, но литературу [5 — 7] трудно назвать общедоступной.
Последнее время в сети Интернет появилось много сообщений о малогабаритных, эффективных и широкополосных антеннах. К сожалению, изложенная теория говорит о том, что создание таких антенн (по крайней мере пассивных) невозможно.
Что же касается малых резонансных антенн, то очень интересна статья [8], в которой автор на качественном уровне приходит к изложенным выше выводам и идет несколько дальше. Анализируя суперпозицию внешнего и собственного поля антенны, он отмечает изменение направления вектора П в сторону антенны, сравнивая ее с «всасывающей воронкой». Описанные эффекты он предлагает в качестве гипотезы, объясняющей работу системы беспроводной передачи энергии Н. Теслы.
Не менее интересна и разработка в рамках проектов НАСА активной низкочастотной рамочной антенны [9, 10], где за счет обратной связи значительно увеличена эффективная поглощающая поверхность при сохранении широкополосности. Эти идеи заслуживают отдельного, более подробного рассмотрения.
Добавление второе — практическое. В других замечаниях отмечалась незавершенность статьи и отсутствие практических выводов. Я хотел предоставить это читателям, поскольку из изложенной теории практически полезных выводов получается много, и объем статьи не позволяет их изложить. Ограничимся одним: оценим эффективную поглощающую поверхность Sэфф и эффективную рассеивающую поверхность Sрасс малой приемной антенны в зависимости от коэффициента рассогласования k = RH/RS.
Будем исходить из простой эквивалентной схемы [1, рис. 3], содержащей последовательно включенные источник сигнала с ЭДС, равной E.hд, сопротивление излучения RS, сопротивление нагрузки Rн, емкость антенны Са и индуктивность «удлиняющей» катушки L. Реактивности положим скомпенсированными при настройке антенны в резонанс. При Rн = RS ,т. е. k = 1 выделяемая в нагрузке мощность равна переизлучаемой:
P0 = E2hд2/4RS.
Подставляя RS = 1600hд2/l2, получаем
P 0 = E 2 l 2/6400.
Sэфф = Sрасс = S0 = Р0/П = 0,06l 2 — уже известный нам результат.
При k = 0 (короткозамкнутая антенна без нагрузки) принятая мощность возрастает вчетверо и вся она переизлучается.
S эфф = 0, S расс = 0,25 l 2.
Для произвольного k имеем мощность в нагрузке
Pн = 4Р0 k/(1+k)2,
переизлучаемую мощность
Ррасс = 4Р0/(1+k)2.
Соответствующие площади получаются делением на П. Любопытно, что
Р н/Р расс = k,
и, соответственно,
Sэфф/Sрасс = k.
Графики зависимости эффективных площадей поглощения и рассеяния в зависимости от коэффициента рассогласования k даны на рис. 8. Подобные же графики, но лишь с очень короткими объяснениями и практически без вывода можно найти в [11] и [12].

Итак, мы видим, что хорошо переизлучает лишь недогруженная антенна без потерь при Rн < RS. При увеличении сопротивления нагрузки (от области максимума отдаваемой антенной мощности при k = 1) переизлучаемая мощность очень резко падает, становясь пренебрежимо малой при Rн >> RS (k >> 1).
Именно этот случай и встречается чаще всего на практике, поскольку сопротивление нагрузки складывается из большого сопротивления потерь и равного ему входного сопротивления приемника (по условию отдачи в приемник максимально возможной мощности). Таким образом, на вопрос, поставленный в заголовке статьи, для большинства радиоприемных антенн можно ответить вполне утвердительно.
ЛИТЕРАТУРА
1. Поляков В. О питании радиоприемников “свободной энергией”. Радио, 1997, № 1, с. 22, 23.
2. Поляков В. “Мистика” коротких антенн. Радио, 2000, № 8, с. 18, 19 и № 9, с. 46.
3. Поляков В. Эквивалентность электрических и магнитных антенн. Радио, 2002, № 11, с.16, 17.
4. Поляков В. Малые антенны: физические ограничения. Радио, 2002, № 10, с. 66, 67.
5. Rudenberg R. Der Emphang Elektrischer Wellen in der Drahtlosen Telegraphie. Annalen der Physik, IV, 25, 1908, s.446...466/
6. Chu. J. Appl. Phys., Dec. 1948.
7. Hansen R. C. Fundamental limitation in antennas. Proc. IEEE, Feb. 1981, vol. 69, № 2.
8. Beaty B. Energy-sucking Radio Antennas, N. Tesla`s Power Receiver. http://www.amasci.com/tesla/tesceive.html.
9. U.S. Patent # 5,296,866 «Active Antenna».
10. Sutton J. F. and Spaniol G. C. The Black Hole Antenna. Proc. of the Int. Tesla Symposium, 1992, см. также http://www.unusualresearch.com/Sutton/sutton.htm.
11. Беньковский З., Липинский Э. Любительские антенны коротких и ультракоротких волн. — М.: Радио и связь, 1983, с. 77.
12. Мейнке Х., Гундлах Ф. В. Радиотехнический справочник, т. 1, с. 288. — М-Л.: ГЭИ, 1961.
Приложение. Элементарный вывод формулы, связывающей резонансный объем поля и КПД антенны. Рассмотрим малую вертикальную антенну (рис. 7,б) высотой h << l, нагруженную верхним диском площадью S и настроенную в резонанс катушкой L. Для упрощения положим hд = h и V = Sh. Эквивалентная схема антенны дана на рис. 9.
По условию согласования входное сопротивление приемника R пр выберем равным сумме сопротивления излучения R S и сопротивления потерь Rпот, а реактивности — равными:
R пр = R S + R пот, XL = X A = X.
Найдем мощность, поступающую в приемник:
Р пр = i 2 R пр = E 2 h 2/4(R S + R пот). При R пот = 0 Рпр 0 = E 2 h 2/4R S.
Тогда КПД: h = Р пр/Р пр0 = R S/(R S + R пот).
Выразим реактивное сопротивление Х через длину волны и размеры антенны, полагая СА = e0 S/h: X = 1/wC = h/2pfe0S. Подставляя f = c/l = 1/lÖe0m0, и учитывая, что Öm0/e0 = 120p, получаем Х = 60lh/S.
Поскольку реальная (измеряемая по полосе пропускания) добротность антенной цепи Q = X/2(R S + R пот), имеем (R S + R пот) = X/2Q. Подставляя это, а также R S = 1600h 2/l 2 в формулу для КПД, получаем:
h = R S/(R S + R пот) = 2QSR S/60lh = 53hSQ/l3 = 53VQ/l3.
Учитывая, что V 0 = l3/53 = 0,5(l/3)3, получаем окончательно:
h = VQ/V0 = Vp/V0.
|
Комментарии
Первое, Вы можете легко убедится, рассмотрев например две антенны Ground Plane: одну из провода 1мм, вторую из трубы 10см. Простой расчет показывает, что ближнее поле антенны из 1мм локализовано в значительно меньшей области пространства (отсюда ее высокая добротность и как следствие ее узкополосность) . Но для приема приходящей плоской волны обе GP антенны будут примерно одинаковаы.
Второе. Можно сделать крайне эффективные антенны разменом заметно меньше длины волны, но лишь для ближних полей (убывающих быстрее 1/r). Например для беспроводной зарядки аккумуляторов.
Первый человек с искуственным сердем Robert Tools, (операция проведена July 2, 2001) Подзаряжал аккумуляторы сердца посредством передатчика/при емника волн ближнего поля. А для волн дальнего поля - там только геометрические размеры (за исключением сред с хитро подобранными свойствами).
Попытаюсь это объяснить наглядно.
С чем связана добротность - с полосой пропускания антенны. Измеряется импеданс антенны в широкой полосе частот из из этого делается вывод о ее широкополосност и.
Теперь, чем определяется импеданс антенны - главным образом структурой ее ближнего поля. Т.е. полей, убывающих быстрее 1/r. В этих полях запасена энергия, та самая ED/2 +BH/2. Но на излучение в дальнем поле это все не влияет (более тонкие эффекты сейчас не рассматриваем). Все почти как в конденсаторах и индуктивностях.
Так вот импеданс определяется главным образом ближним полем. А излучение - дальним. При приеме плоской волны только дальнее поле существенно, куда входят только геометрические размеры.
Поэтому разбито на 3 части. Читать в порядке #1,#2,#3.
если вокруг приемника расставить по всем направлениям
много антенн передатчиков и все их направить на приемник (с соответствующим и фазами),
то да, тогда Вы получите сходящуюся сферическую волну
и принятая мощность не будет зависить от размеров антенны приемника.
Для приема же плоских волн это не так.
Если антенна оптимально согласована,
то чем больше размер антенны тем больше мощность сигнала.
Реально это тоже сферическая волна, но центр ее находится в другом месте, в месте нахождения передатчика,
а в месте приема ее можно считать практически плоской.
Мощность, принятая приемником определяется вектором Пойтинга умноженным на эффективное сечение антенны (или, что тоже самое плотностью энергии электромагнитно го поля умноженной на эффективный объем антенны),
определяемое только ее геометрическими размерами.
То есть мощность сигнала приемника ЗАВИСИТ от размеров антенны приемника.
Когда мощность не будет зависеть- это если Вы будете принимать не плоские, а сферические волны.
Т.е. если Вы создадите сходящуяся сферическую волну с центром в месте нахождения приемника,
E=f(theta)/R exp(i(wt+kR)) (отличается знаком перед kR от расходящейся).
про практические конструкции детекторных приемников.
Очень интересно.
Данная же статья про связь эффективных размеров с добротностью неверна.
Дело в другом. Антенна передатчика, вне зависимости от размеров, излучает сферическую волну. Аплитуда E и H имеет вид f(theta)/R
f- некая функция от углов (определяется диаграммой направленности).
Амплитуда убывает как 1/R с расстоянием до передатчика.
Как вектор Пойтинга ExH, так и плотность энергии поля ED/2+BH/2,
убывают как квадрат амплитуды, т.е как 1/R^2
Электрическое поле расходящейся сферической волны ислученной передатчиком
E=f(theta)/R exp(i(wt-kR))
имеет фазу kR, определяемую исключительно R, расстоянием до передатчика.
см, например.
http://dic.academic.ru/dic.nsf/enc_physics/2920/%D0%A1%D0%A4%D0%95%D0%A0%D0%98%D0%A7%D0%95%D0%A1%D0%9A%D0%90%D0%AF
RSS лента комментариев этой записи